As the name suggests, Simplified Payment Verification (SPV), is actually very simple. For some reason, however, many have struggled to comprehend how the process works and how critically important it is to implement to achieve efficiency in the services you offer.
The underlying parts of Simplified Payment Verification
For years, we have endured the mantra of the ‘Decentralists’ spouting ‘everyone must run their own node’ and ‘you need to verify your transactions’.
Why would you do that when a Merkle proof could give you the exact same level of assurance?
What is a Merkle Proof?
A Merkle Proof is the mechanism by which a data element can be verified to exist within a dataset.
Assume you are given a UTXO, if you can verify its existence within a block, you can verify that its creation has been validated by a miner and the UTXO is indeed legitimate and did at least once contain the funds stated.
This reasoning stands, since there is no way for its generating transaction to be included in a block if it wasn’t valid per the rules of the miner who recorded it in there and the other nodes who accepted it to build upon the block that contained it.
Bitcoin Merkle trees
Hash functions rely upon some very fundamental properties to deliver their utility in the Bitcoin protocol. Regardless of the size of the data object being transformed via the hash function, the unique fixed length digital fingerprint generated remains secure for as long as the hash function remains a secure hash function.
This means, as you construct a Merkle tree out of the transactions that occur on the Bitcoin network, that entire transaction set can be securely summarised by one 32-byte value called the Merkle root.
This Merkle root is expressed in the 80-byte block header. The block header contains the metadata of the block and via the hash of the previous block expressed in each subsequent block header, the blockchain is linked together and secured by proof-of-work.
To date, there exists no mechanism to generate either that 32-byte value of the Merkle root, or the hash of the previous block without the identical values in the identical order as which generated them after hashing in the first place.
Therefore, it is entirely redundant to maintain a full record of all the transactions in order to check the validity of a new transaction when, simply maintaining a complete set of block headers will achieve the same purpose.
This means that a secure record of the blockchain’s integrity can be stored for as little overhead as 4.2 megabytes per year. In addition to that by delegating a small responsibility to users, the inputs to a transaction can be checked against these secure block headers to know whether the funds committed are coming from a valid source.
This is not a complex task. By providing the Merkle path values that allow a receiver to recreate the Merkle root of a given block in an additional data envelope with a transaction, this check (a Merkle proof) can be performed in a fraction of a second.
Due to the efficiency of the Merkle tree as a data verification process, this data envelope will never exceed more than a kilobyte even in the case of blocks with billions of transactions.
This same process would be done internally, in any system that leverages the properties of a Merkle tree to provide an efficient data verification service. It’s not unique to Bitcoin.
Setting the record straight on Bitcoin’s distributed nature
Bitcoin was revolutionary in that it solved the double-spend problem. It did so by introducing a distributed system of nodes connected as a peer-to-peer network. These nodes operated with radical incentivised transparency concerning the transactions they are going to process.
Due to this incentivised behaviour, each node can have confidence in the ordering of transactions and subsequently the ordering of how input funds were spent.
The primary task that a receiver of funds really needs this peer-to-peer network of nodes for is to check whether the funds associated with one of these lightweight Merkle proofs have been spent recently.
They do this by broadcasting a transaction they know commits valid funds to a node which will share it immediately with other nodes and then checking whether a randomly polled subset of these nodes agrees the transaction will be included in their next block.
The importance of Bitcoin’s densely connected, small-world network
When this network of nodes is densely connected, knowing that a few nodes will include this transaction in their next block is as good as knowing that all nodes will include this transaction in their next block.
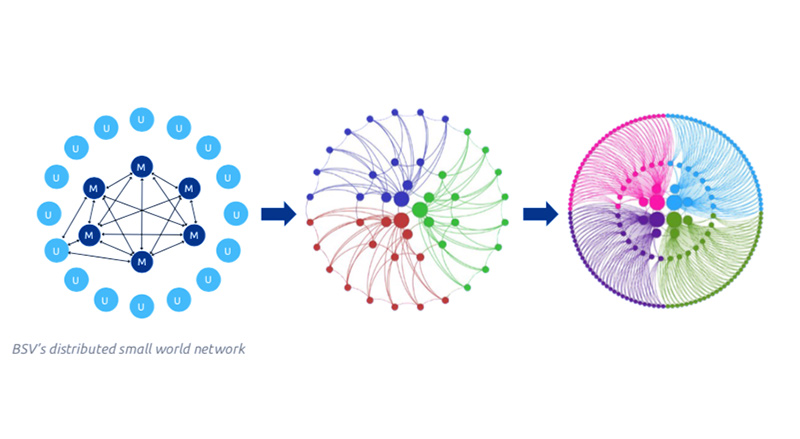
If this network of nodes is loosely connected, with useless entities requesting parasitic connections from legitimate nodes, then that will drain their bandwidth by attempting to have them service these useless nodes which they are not incentivised to do. This has the effect that the system doesn’t work anywhere near as efficiently as it could without the parasites.
By relying on a service that no one has reason to synchronise their records with, you will naturally have a lagging state of the network and its transactions.
When a user thinks they are benefiting the network by hosting a full version of the Blockchain (that needs to have data synced with it from a node who could otherwise allocate resources more effectively to another useful node), then that causes a net loss to that productive node by servicing the useless one.
How running SPV properly puts you ahead of your competitors
Lite wallets that claimed to be running an SPV service yet still run a fully synchronised node client, are operating with one of the daftest business plans imaginable. They run a service which can be offered by competitors for free, with substantial overheads in terms of bandwidth, storage and computational resources, which relies upon the goodwill of highly competitive enterprise-grade machines to stay synchronised with the rest of the network.
All the while this function can be performed in a superior form with no downtime using the resources of the cheapest smartphone on the market or even a specialised IoT field device.
Merkle Trees short course
Learn how to calculate Merkle roots by doing!
The BSV Academy’s new Bitcoin Primitives course focussing on Merkle trees offers you a built-in hash calculator to use during assessments.
As part of our Bitcoin Primitives series, this course is intended to provide students who are new to Bitcoin and without a formal background in computer science a strong foundation in Bitcoin’s fundamental components.
Register for the Merkle Trees short course to learn how Merkle proofs enable BSV blockchain businesses and wallets to implement Simplified Payment Verification (SPV), as described in section 8 of the Bitcoin white paper.